R を使って非線形回帰分析 (nonlinear regression analysis) を行ってみました．ある分布のプロットを，

ロジスティック関数 (logistic model) [glm を使用]
指数関数 (exponential model) [nls を使用]
ゴンペルツ関数 (Gompertz [sigmoidal] model) [nls を使用]

へ回帰します．

Courier の行を R のコンソールに入力してください．「#」で始まる行は，私のコメントです．

# データを入力して，プロットする．

time = c(-353.0, -276.2, -159.2, -153.7,  0,  0, 0, 0)
gene_num = c(96, 40, 37, 37, 29, 25, 27, 28)/96
plot (time, gene_num)

#####################
# ロジスティック曲線への近似 (関数 glm を使用)

# ロジスティック曲線は以下の式で表されます．こちらの P5 をご覧下さい．
# p(x) = exp(a+bx)/(1+exp(a+bx))

# glm = Generalized Linear Model の略．日本語では，一般化線形モデルと呼ばれる．
#「R では一般化線形モデル関数 glm の二項分布を用いてロジスティック回帰分析を行うことができる．」

# ロジスティック回帰は nls でもできるが，glm でやった方が良いらしいです．以下はこちらのサイトに書いてありました．
# 「simplex 法や nls では残差平方和を最小にする解を求めるようになっているのに対して， glm は Deviance を最小にする解を求めるものであるため（普通は，後者を使うべし）」

# 青木先生のページでは，nls で推定する方法も紹介されているようですが，生存率のようなデータには，glm が推奨されています．こちらです．
# 「生存率のように，0~1の値を取るもの（一般的には分布曲線）に曲線を当てはめるには glm を使うようにしましょう」

#「関数nlsでは、線形回帰分析の場合と同じく、被説明変数の実測値と予測値(あるいは推測値)との差を最小とする最小2乗法で係数(パラメータ)を求めている。」 (ref)．
# 「一般化線形モデル (glm) では，最尤法でパラメータ推定を行います」 (ref)．

logisticModel = glm(gene_num ~ time, binomial)

警告メッセージ：
In eval(expr, envir, enclos) : 二項 glm で整数でない成功数がありました!

# 恐らく残差の分布を二項分布にしたため，上のメッセージが出たのだと思います．
# binomial をはずすと正規分布が用いられ，警告メッセージはでません．
# ただし，R では，一般化線形モデル関数 glm の二項分布を用いて
# ロジスティック回帰分析を行うので，binomial にしておく必要があります．
# チルダ「~」は，左辺が右辺の確率分布に従うことを意味しています (ref)．

summary(logisticModel)

Call:
glm(formula = gene_num ~ time, family = binomial)

Deviance Residuals:
Min 1Q Median 3Q Max
-0.46957 -0.15911 0.05048 0.10331 0.76302

Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.105247 1.083793 -1.020 0.308
time -0.006205 0.006063 -1.023 0.306

(Dispersion parameter for binomial family taken to be 1)

Null deviance: 2.06727 on 7 degrees of freedom
Residual deviance: 0.88649 on 6 degrees of freedom
AIC: 11.469

Number of Fisher Scoring iterations: 4

# 推定されたパラメータを出力し，パラメータを変数に格納する．

logisticModel$coefficients
a <- logisticModel$coefficients[1]
b <- logisticModel$coefficients[2]

(Intercept) time
-1.105246661 -0.006204704

#　元の式に戻すと，a=-1.105246661, b=-0.006204704, であるから，
# Logistic model
# Y = exp (a+b*x)/(1+exp(a+b*x))
# = exp (-1.105246661-0.006204704*x)/(1+exp(-1.105246661-0.006204704*x))
# となる

# 回帰曲線の式を入力、グラフ上へプロット．

lineLogistic = function(x) exp (a+b*x)/(1+exp(a+b*x))
plot (lineLogistic, -360, 0, add=TRUE)

#####################
# 指数モデル: 予測式 Y = ab^X への当てはめ（関数nls使用）
# nls = Nonlinear Least Squares の略
# => エクセルを使用した場合は
# y = 26.123e-0.0027x

exponentialModel = nls(gene_num ~ a*b^time, start=list(a=1.0, b=1.0))
summary(exponentialModel)

Formula: gene_num ~ a * b^time

Parameters:
Estimate Std. Error t value Pr(>|t|)
a 0.2349341 0.0493448 4.761 0.00312 **
b 0.9963559 0.0007567 1316.756 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1196 on 6 degrees of freedom

Number of iterations to convergence: 8
Achieved convergence tolerance: 6.444e-06


# 指数モデル Y=ab^X の係数を求めると，係数 a=0.2349341, b=0.9963559 より，
# 指数モデル Y= 0.2349341*0.9963559^X となる．

# 推定されたパラメータの出力し，パラメータを変数に格納する．

(p <- exponentialModel$m$getPars()) ## パラメータを取り出す
a = p[1]
b = p[2]

# 回帰曲線の式を入力、グラフ上へプロット

lineExponential = function(x) a*b^x
plot (lineExponential, -360, 0, add=TRUE, col = "blue")

#####################
# ゴンペルツ成長曲線モデル（sigmoid Gompertz growth model; S字、シグモイド）
# への回帰（関数SSgompertz()を使用）

# ロジスティック曲線は変曲点を中心に左右対称になるが、
# ゴンペルツ曲線は対称性がないのが大きな特徴。

# ゴンペルツ曲線の式は Y= a*b^exp(-c X)

# 関数 SSgompertz は a=Asm, b=exp(-b2), c=-log(b3)，として
# R では Y ~ Asym*exp(-b2 * b3^X)
# としてパラメータを自動的に推定する．

>gompertzModel = nls(gene_num ~ SSgompertz(time, Asym, b2, b3))
>summary(gompertzModel)
Formula: gene_num ~ SSgompertz(time, Asym, b2, b3)

Parameters:
Estimate Std. Error t value Pr(>|t|)
Asym 0.302956 0.023368 12.96 4.87e-05 ***
b2 -0.007806 0.011473 -0.68 0.526
b3 0.985858 0.003998 246.56 2.08e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.0472 on 5 degrees of freedom

Number of iterations to convergence: 21
Achieved convergence tolerance: 7.354e-06

>(p <- gompertzModel$m$getPars()) ## パラメータを取り出す

Asym b2 b3
0.302956192 -0.007805802 0.985858027

# ゴンペルツ成長モデル Y= Asym*exp(-b2 * b3^X) の係数 Asym ,bs, b3 を求めると，
# Asym= 0.302956, b2= -0.007806, b3= 0.985858 である．
# よって関数 SSgompertz より
# Y = Asm * exp(-b2 * b3^X)
# = 0.302956 * exp(-(-0.007806) * 0.985858^X)

(a=Asym=p[1])

0.3029562

(b=exp(-p[2]))

1.007836

(c=-log(p[3]))

0.01424292

#　元の式に戻すと，
# a=Asym=0.302956, b=exp(-b2)=exp(-(-0.007806))=1.007837, c=-log(b3)=0.01424295,
# であるから，
# ゴンペルツ成長モデル
# Y= a * b ^exp(-c X)
# = 0.302956 * 1.007837 ^ exp(-(0.01424295)*X)
# となる

# 回帰曲線の式を入力、グラフ上へプロット

lineGompertz = function(x) a * b ^ exp(-(c)*x)
plot (lineGompertz, -360, 0, add=TRUE, col="red")

#####################
# 赤池情報量基準による「モデルの選択」
# 赤池情報量基準は統計モデルの良さを評価するための指標で，AIC とも呼ばれ，この指標が小さい方が良いモデルと考えられます　(くわしくはこちらを参照してください)．

# 各 AIC 値を計算する

AIC(logisticModel)
AIC(exponentialModel)
AIC(gompertzModel)

# AIC の値で確認すると，ゴンペルツモデルが小さい．このため，ゴンペルツ成長モデル
# Y = 0.302956 * 1.007837 ^ exp(-(0.01424295)*X)
# を回帰式として選択することになります．

######
Excel を使ってグラフの確認をしました．こちらです．

##
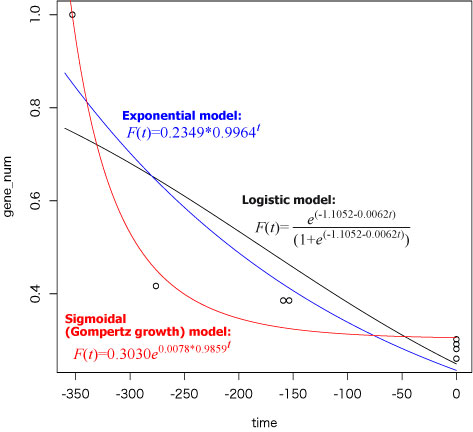
以下のようなプロットが得られているはずです．数式は Illustrator で書き足しました

上述のように nls を使ってロジスティック回帰を行うこともできるようです．nls を用いてロジスティック回帰を行う場合は，こちらによると初期値を選ぶ方法と SSlogis を使う (初期値を必要としない) 方法があります． しかし，ここで使っている例題は，そのままでは解析がストップしてしまいました．そこで，x 軸 (time) のスケールを x0.01 にしたところ，一応，曲線が得られました．以下に関連の解析を示します．なお，上で示した Gompertz でも，スケールを x0.01 にしても問題なく回帰できました．

# Rsolnp というパッケージを使うと，非線形回帰のパラメータ推定がスムーズにできるようですが，私はまだ使ったことがありません．

nraSolver.xlsx

Excel ソルバーを用いて R の nls 解析に用いる初期値を推定
今回はソルバーを使わなくても大丈夫でしたが，解析を上のエクセルファイルに残しておきました．ソルバーの設定はこちら等をご覧下さい．パラメータ設定は以下の画面を参照してください．

#time = c(-353.0, -276.2, -159.2, -153.7, 0, 0, 0, 0)

time = c(-353.0, -276.2, -159.2, -153.7, 0, 0, 0, 0)*0.01
gene_num = c(96, 40, 37, 37, 29, 25, 27, 28)/96
plot (time, gene_num,xlim=c(-8,0), ylim=c(-0.1,1))

######################
# LogisticNSL

dfL1 <- data.frame(x=time, y=gene_num)

# 初期値は Excel のソーバーで推定したが，(b=-1, c= -1) でも今回は大丈夫でした．

logisticNLS <- nls (y ~ 1/(1+exp(-(b+c* time))), dfL1, start=list(b=-30, c= -10))
# logisticNLS <- nls(y ~ SSlogis(x, A, B, C), data= dfL1) # SSlogis はうまくいきませんでした．
summary(logisticNLS)

Formula: y ~ 1/(1 + exp(-(b + c * time)))

Parameters:
Estimate Std. Error t value Pr(>|t|)
b -1.1298 0.3740 -3.021 0.0234 *
c -0.6004 0.2025 -2.965 0.0251 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1499 on 6 degrees of freedom

Number of iterations to convergence: 9
Achieved convergence tolerance: 8.845e-06

(p <- logisticNLS $m$getPars()) ## パラメータを取り出す

b c
-1.1298374 -0.6003967

(b = p[1])

b
-1.129837

(c = p[2])

c
-0.6003967

lineLogistic = function(x) 1/(1+exp(-(b+c*x)))
plot (lineLogistic, -8, 0, add=TRUE)